• Menu
  About Myself Introduction Data Sources Data Visualization Exploratory Data Analysis ARMA/ARIMA/SARIMA Models Financial Time Series Models (ARCH/GARCH) Deep Learning for TS Conclusions

Financial Time Series Models (ARCH/GARCH)

• Inspect Data

	Solar Power	Gas
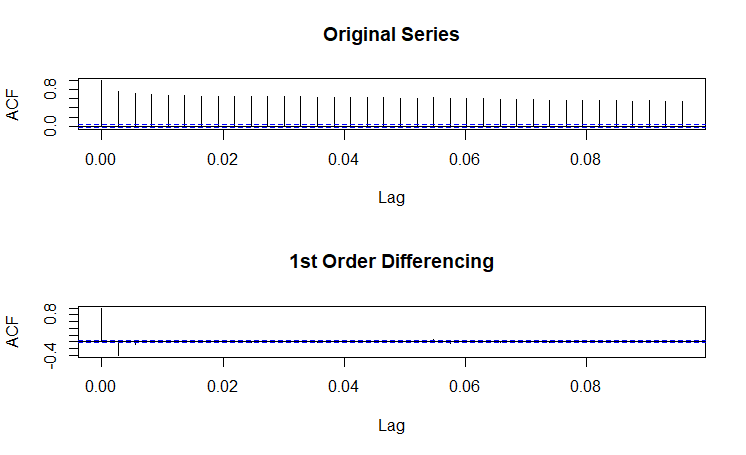
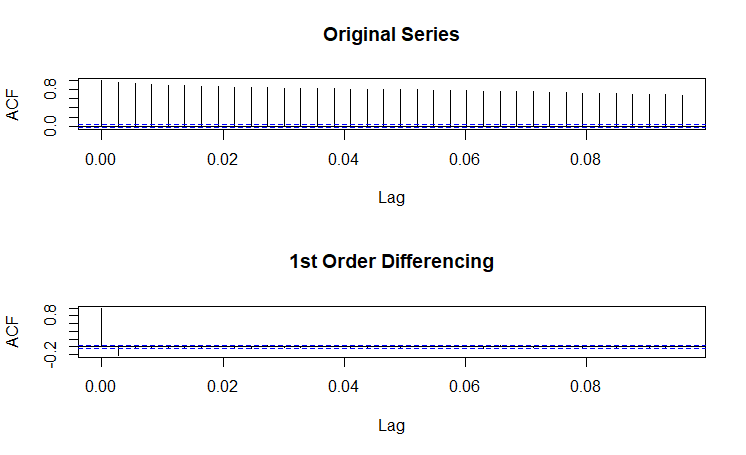
Stationarity	(Click to see a larger view.)	(Click to see a larger view.)
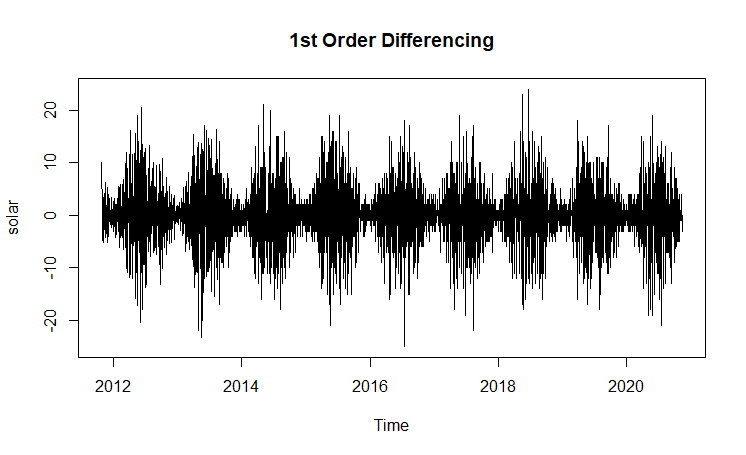
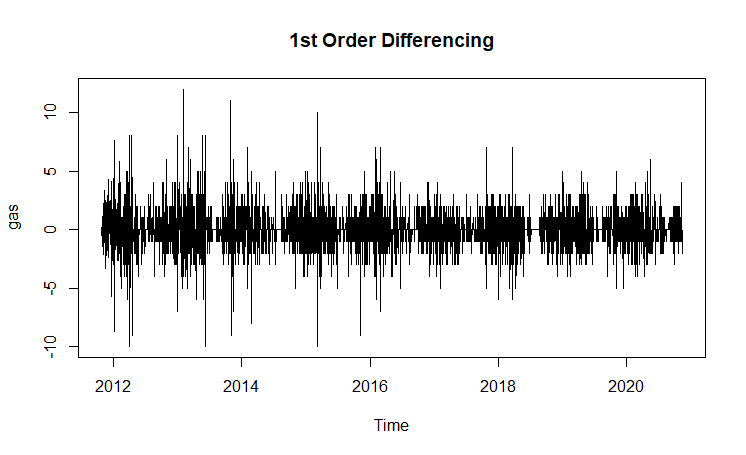
Volatility	(Click to see a larger view.)	(Click to see a larger view.)

The series for both solar power and gas are not stationary, since ACF plots show strong correlations between observations. After 1st order differnecing, both series are stationary. In addition, volatility phenomenon is observed in the plots.

• Decide the order (p,q) of GARCH model

	Solar Power	Gas
ARCH Test	(Click to see a larger view.)	(Click to see a larger view.)
Squared Residuals	(Click to see a larger view.)	(Click to see a larger view.)
ACF Plots	(Click to see a larger view.)	(Click to see a larger view.)
PACF Plots	(Click to see a larger view.)	(Click to see a larger view.)

Following the results of ARIMA models, ARIMA(1,1,1) is fit for solar power data and ARIMA(2,1,1) is fit for gas data. The squared residuals of ARIMA models are checked for determining the GARCH models.

From the ARCH tests, both p-values are less than 0.05, indicating that the series for both solar power and gas have ARCH effect. Therefore, GARCH models will be built. For both solar power and gas data, possible p,q values are [1,2].

• Compare AIC & BIC to find the best model

	Solar Power	Gas
GARCH(1,1)	(Click to see a larger view.)	(Click to see a larger view.)
GARCH(1,2)	(Click to see a larger view.)	(Click to see a larger view.)
GARCH(2,1)	(Click to see a larger view.)	(Click to see a larger view.)

GARCH models are built one by one to compare the AIC and BIC and find the best one. For solar power data, the best GARCH model is GARCH(1,1) according to the lowest AIC and BIC. For gas data, the best GARCH model is GARCH(2,1) according to the lowest AIC and BIC.

• Fit GARCH Models

	Solar Power	Gas
Coefficients	(Click to see a larger view.)	(Click to see a larger view.)
Box-Ljung Tests	(Click to see a larger view.)	(Click to see a larger view.)
Equations	(Click to see a larger view.)	(Click to see a larger view.)

The null hypothesis of Box-Ljung tests is that the data are independently distributed. From the Box-Ljung tests, all of the p-values are larger than 0.05, indicating that there are not enough evidence to reject H0. That is, the correlations in the ARIMA residuals are 0, so that any observed correlations in the data result from randomness of the sampling process.